Rope Optimizations, Part 1

A couple of weeks ago I came across one of Antonio's PRs, titled "Speed up point translation in the Rope" — now who doesn't stop to take a closer look at a PR with that title?

The description already lives up to the title. It contains benchmark results telling me that a method on our Rope named point_to_offset is now up to 70% faster. 70%! Throughput increased by 250%. (I can't remember but I'm sure I made one of those impressed whistling sounds when I saw those numbers.)

Then there's the code. I scrolled through the diff and with the fourth move of the mouse wheel I landed on this snippet and stopped:

#[inline(always)]
fn nth_set_bit_u64(v: u64, mut n: u64) -> u64 {
    let v = v.reverse_bits();
    let mut s: u64 = 64;
 
    // Parallel bit count intermediates
    let a = v - ((v >> 1) & (u64::MAX / 3));
    let b = (a & (u64::MAX / 5)) + ((a >> 2) & (u64::MAX / 5));
    let c = (b + (b >> 4)) & (u64::MAX / 0x11);
    let d = (c + (c >> 8)) & (u64::MAX / 0x101);
 
    // Branchless select
    let t = (d >> 32) + (d >> 48);
    s -= (t.wrapping_sub(n) & 256) >> 3;
    n -= t & (t.wrapping_sub(n) >> 8);
 
    // [...]
}

Okay, okay, okay — "Parallel bit count intermediates", "Branchless select" in a PR that results in a 75% speed up — I'm in. I need to know the whole story. No way this won't be interesting.

So I asked Antonio what's up with the bit twiddling and he not only offered to walk me through the optimizations he made, but also said we should pair and add yet another optimization to make the Rope even faster when handling tabs.

And — lucky me — that's exactly what we did. We recorded the whole pairing session, so you can watch it too, and now I'll share with you everything I learned about bit twiddling optimizations on our Rope so far.

Companion Video: Rope Optimizations, Part 1

The 1.5hr companion video is the full pairing session in which Antonio and Thorsten first walk through these new optimizations on the Rope and then add another one to index tabs.

Watch the video here: https://youtu.be/9Ys9lpOyv08

Speeding up Point translation

First, we let's take a look at how Antonio sped up "point translation" in the Rope and what that even means.

If you've read our post on Rope & SumTree you already know this: our Rope is not a real Rope but a SumTree in a trench coat and looked roughly like this before Antonio made his changes:

struct Rope {
    chunks: SumTree<Chunk>
}
 
struct Chunk(ArrayString<128>);

It's a B-tree of Chunks and a Chunk is nothing more than a stack-allocated string with a maximum length of 128 bytes.

And that's already all the background you need — our Rope is a B-tree of 128-byte strings.

The Problem

So what's point translation? Expressed in code, it's roughly equivalent to this:

struct Point {
    row: u32,
    column: u32,
}
 
impl Rope {
    fn offset_to_point(&self, offset: usize) -> Point;
}

Point translation means: take an arbitrary offset into a string (represented as a Rope) and translate it into a Point — the row and column your cursor would land on if moved to the given offset.

As you can imagine, this method is a popular one in a text editor. Zed gets offsets from all kinds of sources and has to turn them into lines and columns — hundreds if not thousands of times per second when you're moving around a file and editing.

Now imagine how you would implement that offset_to_point method.

Conceptually, what you'd have to do is to go through each character in the file, count the newlines and characters you come across, and stop once you are at your offset. Then you know which line you are on.

And that's exactly what our Rope did, too.

If you called rope.offset_to_point(7234), the Rope would traverse its SumTree to find the Chunk that contains offset 7234 and then, on that Chunk, it would call offset_to_point again. And that method, on Chunk, looked pretty similar to this piece of code:

fn offset_to_point(text: &str, offset: usize) -> Point {
    let mut point = Point { row: 0, column: 0 };
    for (ix, ch) in text.char_indices() {
        if ix == offset {
            break;
        }
        if ch == '\n' {
            point.column = 0;
            point.row += 1;
        } else {
            point.column += 1;
        }
    }
    point
}

It's straightforward: set up a counter in the form of a Point, loop through all the characters in the 128-byte string, and keep track of newlines as you come across them.

But that's also the problem, right there: while the Rope can get us to the right Chunk in O(log(n)), we still have to loop through 128 characters and count the newlines manually — like cavemen.

Now you might say that 128 characters isn't a lot and what harm comes from a little loop like that, but remember: we're talking about a text editor that supports multiple cursors and talks to multiple language servers at once — this loop gets executed so often, it's hot to the touch. We want it to be as fast as possible.

And that's exactly what Antonio achieved.

The Optimization

What Antonio figured out is that instead of looping through 128 characters every time we need find a newline, we can do it once and remember where they are, effectively building an index of the Chunk.

And all we need for such an index is a u128.

A u128 is Rust's 128-bit unsigned integer type and, hey, 128 — that's exactly how many bytes are in a Chunk.

A single u128 is enough to remember whether a given byte in a Chunk has a certain property or not. For example, we could set a bit in a u128 at a given position to 1 if the corresponding byte in the Chunk is a newline character. Or we could flip bits to remember how many bytes a character takes up — which can be more than one with UTF-8 and emojis.

That's what that Antonio's PR did. Our Chunk now looks like this:

struct Chunk {
    chars: u128,
    chars_utf16: u128,
    newlines: u128,
 
    text: ArrayString<128>,
}

But how does that work? And what does it buy us? Is that really better than looping through the characters?

To illustrate the idea, let's focus on newlines only and use a u8 instead of a u128 — less bits to show and count, same principle.

Indexing newlines in a u8

Say we have the following text:

ab\ncd\nef

We can use the following code to index the positions of the newline characters in a u8:

fn main() {
    let text = "ab\ncd\nef";
    let newlines = newline_mask(text);
    // ...
}
 
fn newline_mask(text: &str) -> u8 {
    let mut newlines: u8 = 0;
    for (char_ix, c) in text.char_indices() {
        newlines |= ((c == '\n') as u8) << char_ix;
    }
    newlines
}

When we run this, we end up with a newlines bitmask that looks like this:

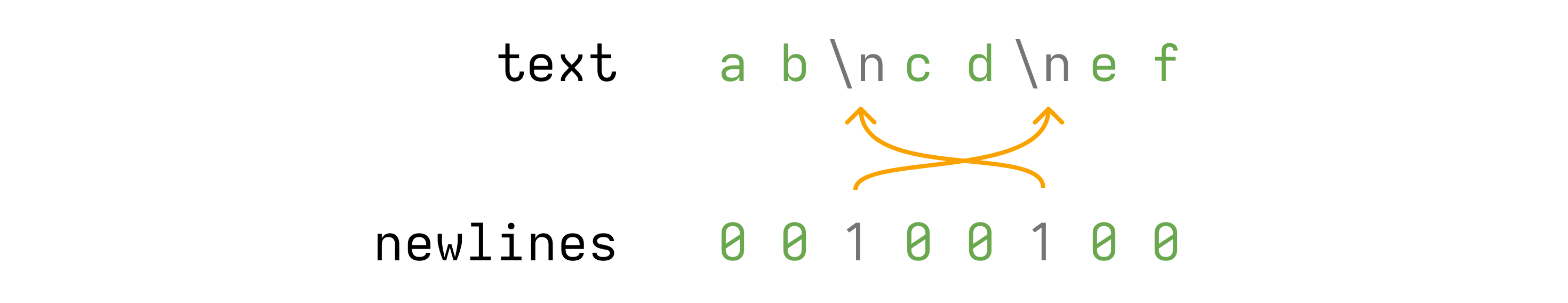
newlines now tells us that the 3rd and 6th characters in text are newlines. Sweet. Now with newlines in hand, back to our original problem: translating an offset into a Point.

How does newlines help with that?

Say our offset is 4 and say our text is "ab\ncd\nef". We want to know what line and column the character d is on.

Here's how we can use newlines to find out:

struct Point { row: u8, column: u8 }
 
fn offset_to_point(newlines: u8, offset: usize) -> Point {
    let mask = if offset == MAX_LEN {
        u8::MAX
    } else {
        (1u8 << offset) - 1
    };
 
    let row = (newlines & mask).count_ones() as u8;
    let newline_ix = u8::BITS - (newlines & mask).leading_zeros();
    let column = (offset - newline_ix as usize) as u8;
 
    Point { row, column }
}

We first create a mask that has all the bits set to 1 up until the offset we're interested in:

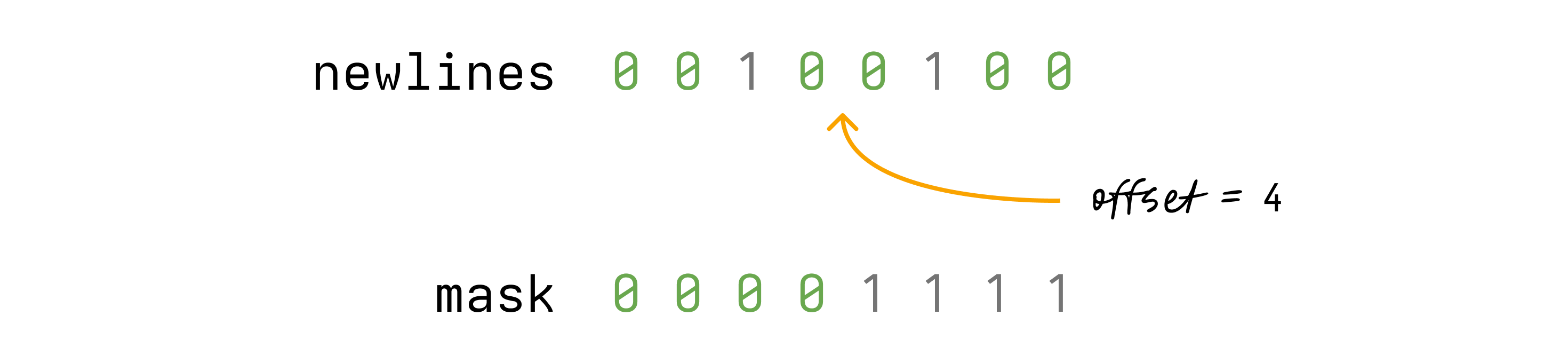
Then we take that mask and bitwise-and it with the newlines we passed in:

That leaves only the newline-bits up to the offset we're interested in being set. Now, to find out which line our offset is on, all we have to do is to count the number of remaining bits set to 1. That's this line:

let row = (newlines & mask).count_ones() as u8; // row = 1

That's the row the offset is on — 1 in our case. It's zero-indexed, meaning that when talking to a human and not a computer, we'd say that the character d is on line 2.

The next step is to figure out the column. To do that, we need to calculate the distance between the offset we're interested in and the last newline character, because that is what a column is: the number of characters from the last newline.

This line first gives us the position of the newline closest to our offset:

let newline_ix = u8::BITS - (newlines & mask).leading_zeros();

In our case, newline_ix is 3:

Then we plug that into the next line:

let column = (offset - newline_ix as usize) as u8;

Which gives us the column 1.

The result: offset 4 in ab\ncd\nef translates to Point { row: 1, column: 1 } — second line, second column.

The Beauty of It

Take a look at these two lines from above again:

let row = (newlines & mask).count_ones() as u8;
let newline_ix = u8::BITS - (newlines & mask).leading_zeros();

count_ones() and leading_zeros() — sounds an awful lot like there might be some looping going on to count those ones and zeros, right?

But no, that's the beautiful part! count_ones and leading_zeros are both implemented with a single CPU instructions. No loop necessary. Turns out CPUs are pretty good with zeros and ones.

And it's not just that we reduced the number of instructions, we also have less branch instructions now and branchless programming can often lead to tremendous speed-ups in hot loops.

If we put both versions of offset_to_point — one with a loop and one with the bitmask — into micro-benchmark and use an actual u128 instead of an u8 to make the results more pronounced, we can see how much faster the loop-less, branch-less version is:

Running benches/benchmark.rs (target/release/deps/benchmark-21888b29446a33c0)

offset_to_point_u128/loop_version
                   time:   [56.914 ns 57.001 ns 57.096 ns]

offset_to_point_u128/mask_version
                   time:   [1.0478 ns 1.0501 ns 1.0529 ns]

57ns with the loop and 1ns with the bitmask — 57x faster. Impressed whistling sound.

Of course, all the disclaimers about micro-benchmarks apply and in our production code the results aren't that drastic, but very, very good nonetheless: the 70% speed-up I mentioned at the start is real.

Indexing Tabs

Fascinated and motivated by all of this, Antonio and I then set out to add the same index for tabs.

"Tabs?", you might say, "I don't use tabs." Yes, you don't, but Zed doesn't know that and still has to check whether you have tabs at the start of your lines in order to display them correctly.

And tabs are tricky. You can't display tabs like other characters. Tabs are... dynamic, for the lack of a better word.

How the string \t\tmy function is displayed depends on what tab size you have configured: if the tab size is four, then \t\t should be displayed as eight spaces. If it's two, it's four spaces.

"Poor text editor developers", you might be thinking, "they have to multiply numbers." Appreciate the compassion, but, listen, that's not all.

Consider this piece of text:

ab\t\tline 1
\t\tline 2

With a tab size of 4 and hard tabs enabled, it should be displayed like this:

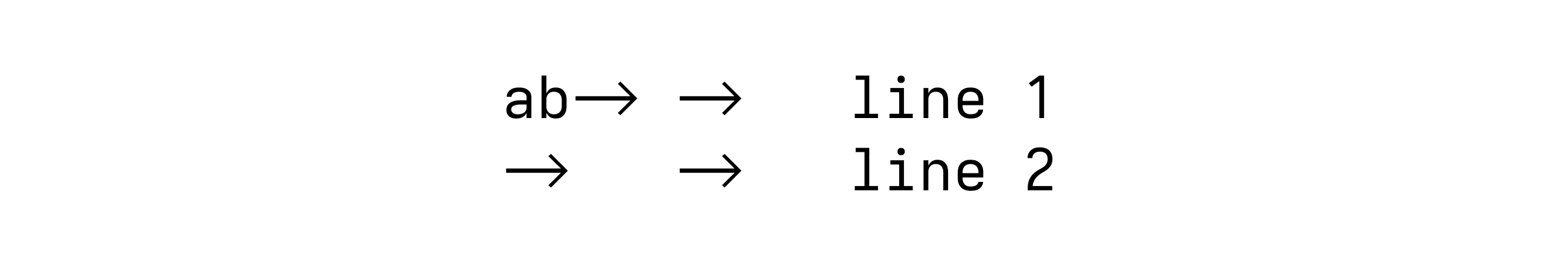
That's right — the first tab in the first line only takes up two spaces, the others all take up four spaces.

You see: tabs are tricky and, as it turns out, also costly.

In a performance profile, Antonio saw that we spend a lot of time figuring out where and how many tabs there are in a given file. A lot of time.

So what we did in our pairing session was to add an index for tabs that works just like the index for newlines:

struct Chunk {
    chars: u128,
    chars_utf16: u128,
    newlines: u128,
 
    // We added this field:
    tabs: u128
 
    text: ArrayString<128>,
}

Does it make Zed faster?

We'll see. This time we only added the index, but we haven't actually changed the code the higher layers to use it yet. We'll do that in the next Zed Decoded episode.

Until then, watch the full pairing session in the companion video to see how all the nuts and bolts are put into place.